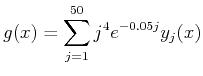Highly Nonlinear Approximations for Sparse Signal Representation

Logo EPSRC
next next up previous
Next: Recursive updating/downdating of oblique Up: The need of nonlinear Previous: The need of nonlinear

Example 5

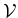
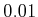
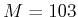
Let $ {\cal{V}}$ be the cardinal cubic spline space with distance $ 0.01$ between consecutive knots, on the interval $ [0,1]$. This is a subspace of dimension $ M=103$, which we span using a B-spline basis

$\displaystyle B=\{B_i(x), x\in [0,1]\}_{i=1}^{103}$

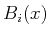
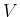
The functions $ B_i(x)$ in $ V$ are obtained by translations of a prototype function and the restriction to the interval $ [0,1]$. A few of such functions are plotted in the left graph of Fig. 3.

Figure 3: Left graph: cubic B spline functions, in the rage $ x \in [0.1, 0.3]$, from the set spanning the space of the signal response. Right graph: tree of the functions spanning the space of the background.
\includegraphics[width=8cm]{spli2.eps} \includegraphics[width=8cm]{gbac.eps}

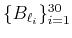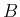Taking, randomly, 30 B-splines $ \{B_{\ell_i}\}_{i=1}^{30}$ from $ B$ we simulate a signal by a weighted superposition of such functions, i.e.,

$\displaystyle f_{\cal{V}}(x)=\sum_{i=1}^{30} c_{\ell_i} B_{\ell_i}(x),\quad x\in [0,1],$ (15)

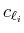
with the coefficients $ c_{\ell_i}$ randomly chosen from $ [0,1]$.

We simulate a background by considering it belongs to the subspace 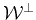$ {\cal{W}^\bot}$ spanned by the set of functions

$\displaystyle Y=\{y_j(x)=(x+0.01 j)^{-0.01 j}, x\in [0, 1]\}_{j=1}^{50}.$

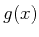
A few functions from this set are plotted in the right graph of Fig. 3 (normalized to unity on $ [0, 1])$. The background, $ g(x)$ is generated by the linear combination

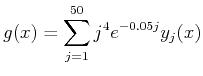$\displaystyle g(x)= \sum_{j=1}^{50} j^4e^{-0.05j}y_j(x)$ (16)

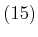
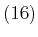
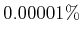
To simulate the data we have perturbed the superposition of $ \eqref{sir}$ and $ \eqref{bac}$, by `very small' Gaussian errors (of variance up to $ 0.00001\%$ the value of each data point). The simulated data are plotted in the left graph of Fig. 4.

This example is very illustrative of how sensitive to errors the oblique projection is. The subspace we are dealing with are disjoint: the last five singular values of operator 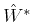$ \hat{W}^\ast$ (c.f. (11)) are:

$\displaystyle 0.3277, 0.3276, 1.0488 \times 10^{-4}, 6.9356 \times 10^{-8}, 2.3367 \times 10^{-10},$

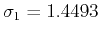
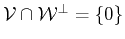
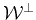
while the first is $ \sigma_1=1.4493$. The smallest singular value cannot be considered a numerical representation of zero, when the calculations are being carried out in double precision arithmetic. Hence, one can assert that the condition $ {\cal{V}}\cap {\cal{W}^\bot}= \{0\}$ is fulfilled. 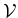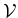However, due to the three small singular values the oblique projector along $ {\cal{W}^\bot}$ onto the whole subspace $ {\cal{V}}$ is very unstable, which causes the failure to correctly separate signals in $ {\cal{V}}$ from the background. The result of applying the oblique projector onto the signal of the left graph is represented by the broken line in the right graph. As can be observed, the projection does not yield the required signal, which is represented by the continuous dark line in the same graph. Now, since the spectrum of singular values has a clear jump (the last three singular values are far from the previous ones) it might seem that one could regularize the projection by truncation of singular values. Nevertheless, such a methodology turns out to be not appropriate for the present problem, as it does not yield the correct separation. Propositions 3 below analyzes the effect that regularization by truncation of singular values produces in the resulting projection.

Figure 4: Left graph: signal plus background. Right graph: the dark continuous line corresponds to the signal to be discriminated from the one in the left graph. The broken line corresponds to the approximation resulting from the oblique projection. The three closed lines correspond to the approximations obtained by truncation of one, two, and three singular values.
\includegraphics[width=8cm]{exasigo3.eps} \includegraphics[width=8cm]{exatrun2.eps}

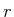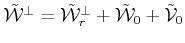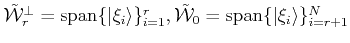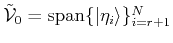Proposition 3   Truncation of the expansion (13) to consider up to $ r$ terms, produces an oblique projector along $ \tilde {{\cal{W}}}^\bot=\tilde {{\cal{W}}}_r^\bot + \tilde {{\cal{W}}}_0+ \tilde {{\cal{V}}}_0$, with $ \tilde {{\cal{W}}}_r^\bot = {\mbox{\rm {span}}}\{\vert\xi_i\rangle \}_{i=1}^r, \tilde {{\cal{W}}}_0= {\mbox{\rm {span}}}\{\vert\xi_i\rangle \}_{i=r+1}^N$ and $ \tilde {{\cal{V}}}_0= {\mbox{\rm {span}}}\{\vert\eta_i\rangle \}_{i=r+1}^N$ onto $ \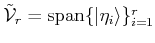tilde {{\cal{V}}}_r= {\mbox{\rm {span}}}\{\vert\eta_i\rangle \}_{i=1}^r$.

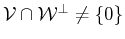
The proof of these propositions can be found in [7] Appendix B. For complete studies of a projector when $ {\cal{V}}\cap {\cal{W}^\bot}\neq \{0\}$ see [8] and [9].

This example illustrates, very clearly, the need for nonlinear approaches: We know that a unique and stable solution does exist, since the signal which is to be discriminated from the background actually belongs to a subspace of the given spline space, and the construction of the oblique projectors onto such a subspace is well posed. Whoever, the lack of knowledge about the subspace prevents the separation of the signal components by a linear operation. A possibility to tackle the problem is to transform it into the one of finding the subspace to which the sought signal component belongs to. In this way the problem can be addressed by nonlinear techniques.

next next up previous
Next: Recursive updating/downdating of oblique Up: The need of nonlinear Previous: The need of nonlinear