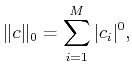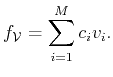Sparse representation by minimization of the norm like quantity - Handling the ill posed case.

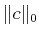
The problem of finding the sparsest representation of a signal for a given dictionary is equivalent to minimization of the zero norm $\Vert c\Vert _0$ (or counting measure) which is defined as:

$\displaystyle \Vert c\Vert _0= \sum_{i=1}^M \vert c_i\vert^0,$

where

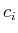
are the coefficients of the atomic decomposition

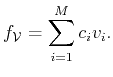$\displaystyle f_{\cal{V}}=\sum_{i=1}^M c_i v_i.$

(29)

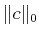
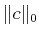
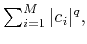
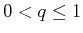
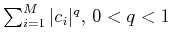
Thus, $\Vert c\Vert _0$ is equal to the number of nonzero coefficients in (29). However, sice minimization of $\Vert c\Vert _0$ is numerically intractable, the minimization of $\sum_{i=1}^M \vert c_i\vert^q,$ for $0 < q \le 1$ has been considered [16]. 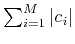Because the minimization of $\sum_{i=1}^M \vert c_i\vert^q, 0 < q <1$ does not lead to a convex optimization problem, the most popular norm to minimize, when a sparse solution is required, is the 1-norm $\sum_{i=1}^M \vert c_i\vert$ . 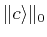Minimization of the 1-norm is considered the best convex approximant to the minimizer of $\Vert c\rangle \Vert _0$ [17,18]. 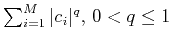In the context of signals splitting already stated, we are not particularly concerned about convexity so we have considered the minimization of $\sum_{i=1}^M \vert c_i\vert^q, 0 < q \le 1$ , allowing for uncertainty in the available data [7]. This was implemented by a recursive process for incorporating constrains, which is equivalent to the procedure introduced in [19] and applied in [20].

Subsections

Managing the constraints
- Numerical Simulation

Highly Nonlinear Approximations for Sparse Signal Representation

Sparse representation by minimization of the norm like quantity - Handling the ill posed case.