Highly Nonlinear Approximations for Sparse Signal Representation
Sparsity and `something else'
We present here a `bonus' of sparse representations by alerting that they can be used for embedding information. Certainly, since a sparse representation entails a projection onto a subspace of lower dimensionality, it generates a null space. This feature suggests the possibility of using the created space for storing data. In particular, in a work with James Bowley [35], we discuss an application involving the null space yielded by the sparse representation of an image, for storing part of the image itself. We term this application `Image Folding'.
Consider that by an appropriate technique one finds a
sparse representation of an image.
Let
![]() be
the
be
the ![]() -dictionary's atoms rendering such a representation
and
-dictionary's atoms rendering such a representation
and
![]() the space they span. The sparsity
property of a representation implies that
the space they span. The sparsity
property of a representation implies that
![]() is a subspace considerably smaller
than the image space
is a subspace considerably smaller
than the image space
![]() .
We can then construct a complementary subspace
.
We can then construct a complementary subspace
![]() , such that
, such that
![]() , and compute the
dual vectors
, and compute the
dual vectors
![]() yielding the
oblique projection onto
yielding the
oblique projection onto
![]() along
along
![]() . Thus,
the coefficients of the sparse representation can be
calculated as:
. Thus,
the coefficients of the sparse representation can be
calculated as:
Now, if we take a vector in
This suggests the possibility of using the sparse representation of an image to embed the image with additional information stored in the vector
Embedding Scheme
We can embed ![]() numbers
numbers
![]() into a vectors
into a vectors
![]() as follows.
as follows.
- Take an orthonormal basis
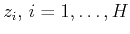 for
for
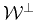 and
form vector
and
form vector 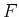 as the linear combination
as the linear combination
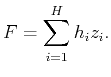
- Add
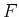 to
to 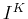 to obtain
to obtain 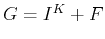
Information Retrieval
Given ![]() retrieve the numbers
retrieve the numbers
![]() as follows.
as follows.
- Use
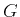 to compute the coefficients of the sparse representation of
to compute the coefficients of the sparse representation of
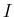 as in (38). Use this coefficients to reconstruct the
image
as in (38). Use this coefficients to reconstruct the
image
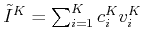
- Obtain
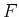 from the given
from the given 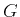 and the reconstructed
and the reconstructed
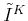 as
as
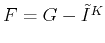 . Use
. Use 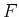 and the orthonormal
basis
and the orthonormal
basis
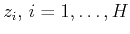 to retrieve
the embedded numbers
to retrieve
the embedded numbers
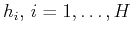 as
as
Subsections

