Suppose that the chirp signal in the first
graph of Fig.
1 is corrupted by
impulsive noise belonging to the subspace
The chirp after being corrupted by a realization of the
noise consisting of
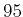
pulses taken randomly from elements
of
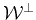
is plotted in the
second graph of Fig.
1.
Consider that the signal subspace is well represented by 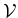 given by
given by
In order to eliminate the impulsive noise from the chirp we
have to compute the measurement vectors
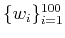
,
here functions of
![$ t\in [0,1]$](img256.png)
, determining the
appropriate projector. For this we first need a representation of
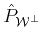
, which is obtained simply by transforming the
set
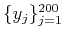
into an orthonormal set
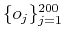
to have
The function for constructing an orthogonal
projector in a number of different ways is
OrthProj.m.
With
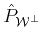 we construct vectors
we construct vectors
The inner products involved in the above
equations and in
the elements,
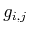
, of matrix
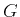
are computed numerically.
This matrix has an inverse, which is used to obtain functions
![$ \{w_i(t), t\in [0,1]\}_{i=1}^{100}$](img264.png)
giving rise to the
required oblique projector.
The chirp filtered by such a projector
is depicted in the last graph of Fig.
1.
Figure 1:
Chirp signal (first graph). Chirp corrupted by
95 randomly taken pulses (middle graph).
Chirp denoised by oblique projection (last graph).
|
|
![]() given by
given by
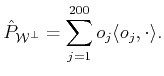
![]() we construct vectors
we construct vectors
![$\displaystyle u_{i+1}(t)=\cos{\pi i t} - \sum_{j=1}^{200} o_j(t) \langle o_j(t), \cos{\pi i t}\rangle ,
\;\;\; i=0,\ldots,99, \;\; t\in [0,1].$](img261.png)
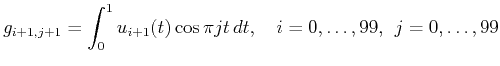
![\includegraphics[width=5.6cm]{chi.eps}](img265.png)
![\includegraphics[width=5.6cm]{chi95.eps}](img266.png)
![\includegraphics[width=5.6cm]{chifil.eps}](img267.png)

