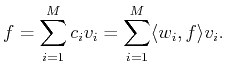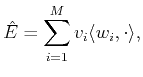Signal Representation, Reconstruction, and Projection

Regardless of its informational content, in this tutorial we consider that a signal is an element of an inner product space $\cal{H}$ with norm induced by the inner product, $\Vert\cdot\Vert= \langle \cdot, \cdot \rangle ^{\frac{1}{2}}$ . Moreover, we assume that all the signals of interest belong to some finite dimensional subspace ${\cal{V}}$ of $\cal{H}$ spanned by the set $\{v_i \in {\cal{H}} \}_{i=1}^M$ . Hence, a signal

can be expressed by a finite linear superposition

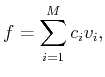
$\displaystyle f= \sum_{i=1}^M c_i v_i,$

where the coefficients $c_i, i=1,\ldots,M$ , are in $\mathbb{F}$ .

We call measurement or sampling to the process of transforming a signal into a number. Hence a measure or sample is a functional. Because we restrict considerations to linear measures the associated functional is linear and can be expressed as

$\displaystyle m= \langle w , f \rangle$ for some $\displaystyle \quad w \in \cal{H}.$

We refer the vector

to as measurement vector.

Considering measurements $m_i, i=1,\ldots,M$ , each of which is obtained by a measurement vector , we have a numerical representation of as given by

$\displaystyle m_i= \langle w_i , f \rangle ,\quad i=1,\ldots,M.$

Now we want to answer the question as to whether it is possible to reconstruct $f\in {\cal{V}}$ from these measurements. More precisely, we wish to find the requirements we need to impose upon the measurement vectors $w_i, i=1,\ldots,M$ , so as to use the concomitant measures $\langle w_i , f \rangle , i=1,\ldots,M$ , as coefficients for the signal reconstruction, i.e., we wish to have

$\displaystyle f= \sum_{i=1}^M c_i v_i= \sum_{i=1}^M \langle w_i , f \rangle v_i.$

(1)

By denoting

$\displaystyle \hat{E}= \sum_{i=1}^M v_i \langle w_i , \cdot \rangle ,$

(2)

where the operation $\langle w_i , \cdot \rangle$ indicates that $\hat{E}$ acts by taking inner products, (1) is written as

$\displaystyle f= \hat{E} f.$

As will be discussed next, the above equation tells us that the measurement vectors $w_i, i=1,\ldots,M$ , should be such that the operator $\hat{E}$ is a projector onto ${\cal{V}}$ .

Subsections

Highly Nonlinear Approximations for Sparse Signal Representation

Signal Representation, Reconstruction, and Projection